What is Big O Notation?
If you’ve taken courses related to algorithms, you’ve heard of the term Big O notation, in a nutshell, Big O is a way of classifying how scalable your function or algorithm is, how your code will perform if the number of values input increase? Constant? Linear? Exponential?
Big O notation is an important topic and its universal importance stems from the fact that it describes the efficiency of code written in any programming language.
Types of Complexities
Big O is used to describe possible scenario complexity. We have the measure that calculates the time required for the execution and the space, which is the total memory used.
With this, the code can have very different complexities, for example, a code that copies the contents of an array to another takes much more time and resources than one that changes an index only, so its complexity will be greater.
Constant : O(1)
Functions that have the same amount of time to process, regardless of how many input elements will be sent. For example, if a function takes the same time to process 1 or 100,000 elements, we say it has a constant growth rate or O(1).
An example is if we try to find the first item in an array, no matter how many items.

Logarithmic: O(log n)
Logarithmic time complexity is characterized by building algorithms that divide the work area in half at each iteration. Consequently, the running time of the algorithm is proportional to the number of times “n” can be divided by 2.
For a list of 16 items, it will take up to 4 steps to complete:
log2 16 = 4
The coolest thing is that if we double the total number of items we will only increase one step in this process:
log2 32 = 5
Binary search is an example of this usage.

Linear: O(n)
This algorithm is based on visiting each element of a list. The O(n) linear time complexity means that the processing time increases proportionally as the number of elements gets larger.
Linear search uses this complexity.

Linearithmic: O(n log n)
When an algorithm performs logarithmic operations n times, it is said to have a linearithmic complexity.
Merge sort is a popular example of linearithmic complexity.

Quadratic: O(n²)
A function with quadratic time complexity has a growth rate of n². If the input is size 2 (two), it will do 4 (four) operations. If the input size is 8, it will be 64, and so on.
We can see an example with bubble sort.

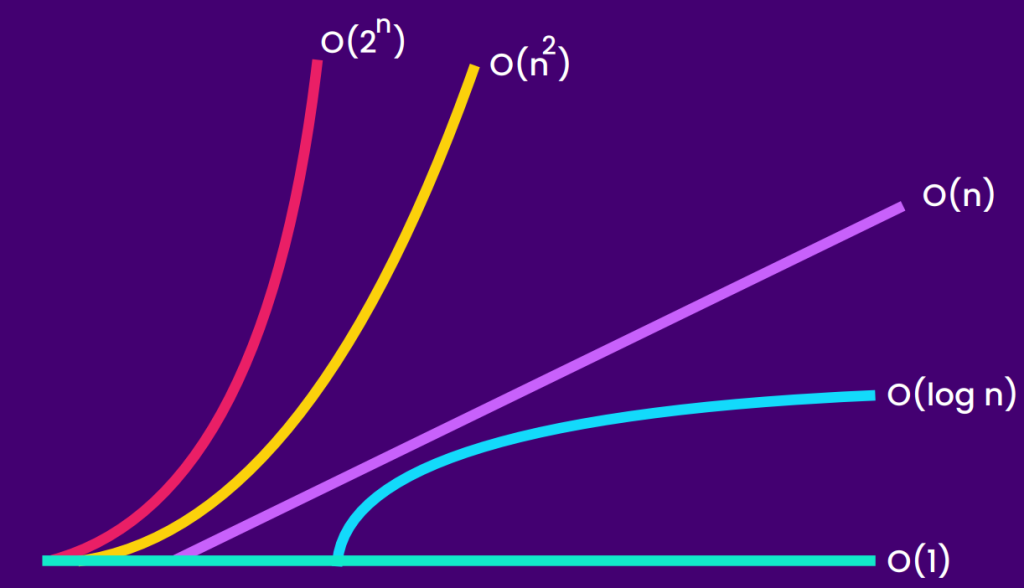
Order of Complexities
To define from least complex to most, we have the following order:
- O(1) - Constant.
- O(log n) - Logarithmic.
- O(n) - Linear.
- O(n log n) - Linearithmic.
- O(n²) - Quadratic.
Finishing
We can still have less efficient algorithms like O(nm), O(2n) or O(n!) but they are so inefficient that they should be avoided, if possible.
Can you find a specific input where an O(n) function performs faster than an O(1) function?
Of course, after all complexity gives us the worst case scenario, but in the best case a higher complexity function can be the same or even better, but in general the greater the complexity, greater the time and resources used.