O que é Big O Notation?
Se você já fez cursos relacionados com algoritmos, já ouviu falar do termo notação Big O, em poucas palavras, Big O é uma forma de classificar quanto a sua função ou algoritmo é escalável, qual será a performance do seu código se o número de valores de entrada aumentar? Constante? Linear? Exponencial?
A notação Big O é um tópico importante e sua importância universal origina-se do fato de descrever a eficiência do código escrito em qualquer linguagem de programação.
Tipos de complexidades
Big O é utilizada para descrever a complexidade cenário possível. Temos a medida que calcula o tempo necessário para a execução e o espaço, que é o total de memória e processamento gasto.
Com isso o código pode ter complexidades muito diferentes, por exemplo, um código que copia o conteúdo de uma array para outra gasta muito mais tempo e processamento do que um que altera um index apenas, logo, sua complexidade será maior.
Constante : O(1)
Identifica as funções que tenham o mesmo tempo para serem processadas, independentemente de quantos elementos de entradas serão enviados. Por exemplo, se uma função leva o mesmo tempo para processar 1 ou 100 mil elementos, dizemos que ela tem uma taxa de crescimento constante ou O(1).
Um exemplo é se tentamos localizar o primeiro item de uma array, não importa a quantidade de intens.

Logarítmico: O(log n)
Complexidade de tempo logarítmico tem como característica construir algoritmos que dividem a área de trabalho ao meio a cada iteração. Consequentemente, o tempo de execução do algoritmo é proporcional ao número de vezes que “n” pode ser dividido por 2.
Para uma lista de 16 itens, serão necessário até 4 etapas para finalizar:
log2 16 = 4
O mais legal é que se dobrarmos o total de itens aumentaremos apenas um passo nesse processo:
log2 32 = 5
A busca binária é um exemplo dessa utilização.

Linear: O(n)
Esse algoritmo tem como base a visita em cada elemento de uma lista. A complexidade de tempo linear O(n) significa que o tempo de processamento aumenta proporcionalmente à medida que a quantidade de elementos fique maior.
A busca linear utiliza essa complexidade.

Linearítmica: O(n log n)
Quando um algoritmo executa operações logarítmicas n vezes, dizemos que ele tem uma complexidade linearitmica.
Merge sort é um exemplo popular de complexidade linearitmica.

Quadrático: O(n²)
Uma função com complexidade de tempo quadrática tem uma taxa de crescimento de n². Se a entrada for tamanho 2 (dois), ele fará 4 (quatro) operações. Se o tamanho da entrada for 8, será 64 e assim por diante.
Podemos ver um exemplo com bubble sort.

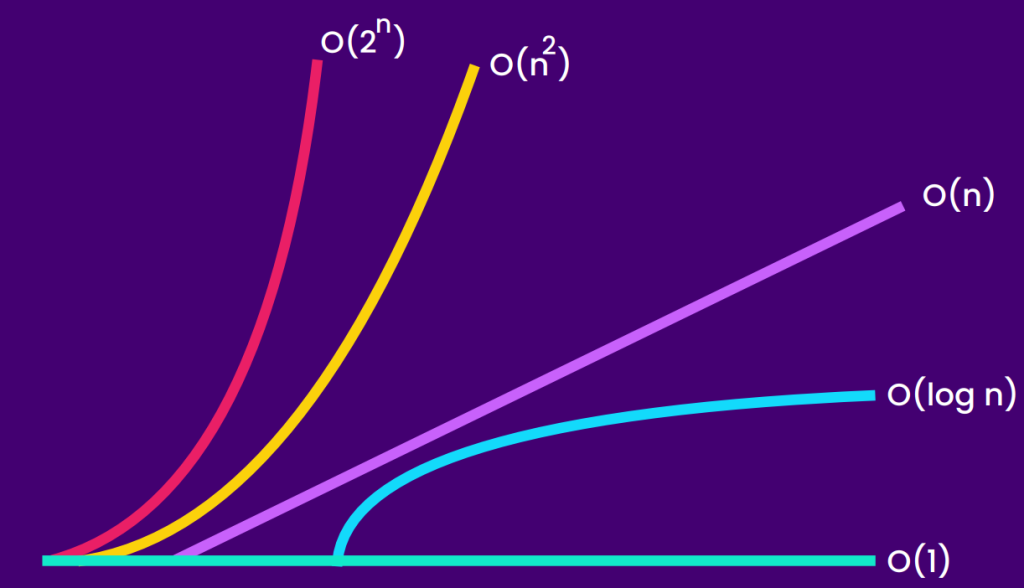
Ordem de complexidades
Para definirmos da menos complexa para a mais, temos a seguinte ordem:
- O(1) - Constante.
- O(log n) - Logarítmico.
- O(n) - Linear.
- O(n log n) - Linearítmica.
- O(n²) - Quadrático.
Finalizando
Ainda podemos ter algorítimos menos eficientes como O(nm), O(2n) ou O(n!) mas são tão ineficientes que devem ser evitados, se possível.
É possível encontrar uma entrada específica em que uma função O(n) performe mais rapidamente do que a função O(1) ?
Claro, afinal a complexidade nos dá o pior cenário, mas no melhor cenário uma função de complexidade maior pode ser igual ou até melhor, mas no geral quanto maior a complexidade, maior o tempo e recursos utilizados.